Feature superposition, co-occurrence and output influence in LLMs: a sparse autoencoder-based analysis
There seems to be tension in the literature between two phenomena of feature superposition in neural networks, which was (and still kind of is) confusing to me.
(1) From Anthropic’s Toy Models of Superposition:
- Two features that do not co-occur will take similar bases in activation space (but are measured in opposite directions) and are decoupled with the nonlinear activation function.
- Two feature that do co-occur will take orthogonal bases in activation space. They will not share a basis as doing so leads to interference when the features occur together.
(2) On the other hand, from Anthropic’s Toward Monosemanticity:
- Two features which correlate to similar downstream neural network outputs (i.e. have similar “output actions”) will take similar bases in activation space. This is because isolating these features is not important when they both ultimately correspond to the same output action; some interference is okay.
However, these two phenomena are somewhat contradictory because wouldn’t we expect that features that co-occur will also have similar output actions? The authors of (2) acknowledge this tension.
I attempted to resolve these phenomena by training an SAE on a 6.3M parameter LLM. Here is my analysis. I discovered a rough heuristic for the cosine between the directions of any two features that considers both correlation and downstream output similarity. Here are the rough results:
| features DO NOT cooccur | features DO cooccur | |
|---|---|---|
| output distribution SIMILAR | cos < 0 | cos > 0 |
| output distribution DIFFERENT | cos < 0 | cos = 0 |
Which was gathered from this plot:
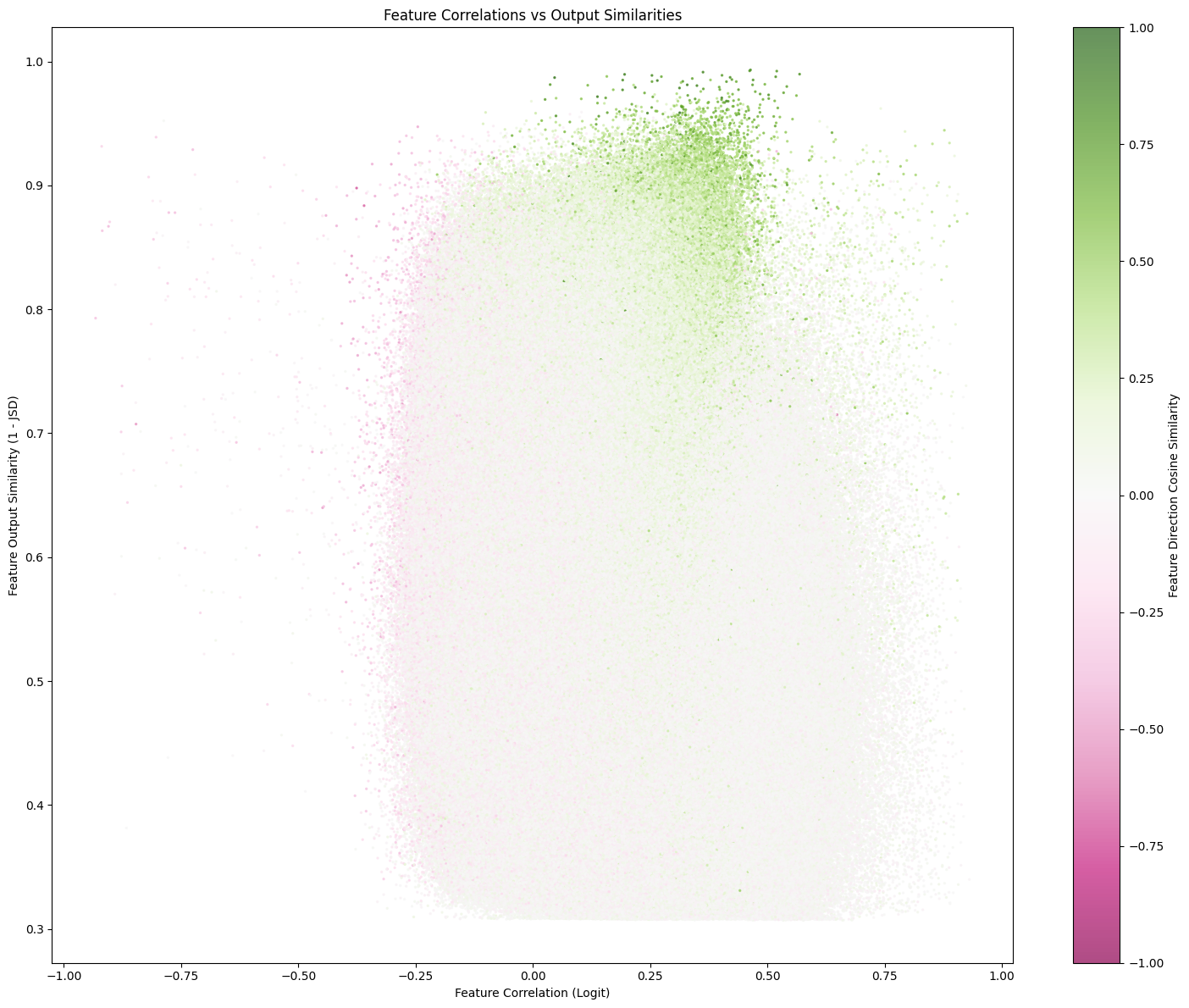
This makes some sense:
- If two features cooccur but yield different outputs, they must take mutually orthogonal bases to avoid interference.
- If two features cooccur and have the same output, then they can take a similar basis because it’s okay to have interference between them (as they both yield the same output).
- If two features do not cooccur, then they can share a basis (superposition), such as by forming antipodal pairs.
What’s still a bit confusing:
- Why do we see such a big splotch of orthogonal feature directions? There can only be so many orthogonal pairs, which is why we see superposition in the first place. Maybe, our analysis needs to be more sensitive to small alignments / antialignments.
- Why would the model choose to use superposition for features that do not cooccur, but cause the same output? Although superposition saves capacity, it costs even fewer parameters to just share the exact same basis (i.e. with the same sign too).