Deep sparse autoencoders for neural network interpretability
This post contains a bunch of introductory philosophical preamble before presenting the actual results, so skip to the results section if you’d like to cut to the chase.
Motivations and intuitions
Levels of abstraction
At NeurIPS 2024, Zico Kolter gave a talk titled “Is this really science? A lukewarm defense of alchemy”. In it, someone (I think it might have been Surya Ganguli, but I’m not confident about this) asked him if he thinks we could ever understand neural networks in a scientific way. To the best of my memory, Zico responded with something along the lines of yes, but that he doesn’t think we’re thinking about deep learning science at the right level of abstraction. I believe he also said something about how thinking at a higher level of abstraction to reason about neural networks might not look like “science” as we’re used to it. The recording of this talk is posted here, but I’m too lazy to go back and confirm my paraphrasing.
I think that this question about how to think at the right level of abstraction is particularly relevant for deep learning, and especially deep learning interpretability. After all, when we say that we want to “understand” how a neural network really operates, why are we not satisfied with the weights of the neural network, of which we are virtually certain? I think this could partially come down to translating these mechanisms into a level of abstraction that our human minds can operate on.
Sparse autoencoders
Sparse autoencoders have been a remarkably successful approach to understanding the internal states of a neural network. The question of why they work so well has interested me quite a bit.
The standard theory behind the success of SAEs (and motivation behind the initiation of the project) is that neural networks fundamentally operate by storing linear “features”, which are just directions in neuron activation space, which are then transformed through the forward pass of the network. To store more features than the network has neurons, the network employs “superposition”, whereby a single neuron can represent multiple features. The sparse autoencoder works, then, by imposing a sparsity constraint that separates these features and extracts them out of their superposed state, and thus allows us to examine and interpret them. This theory is laid out in Anthropic’s Toy models of superposition work.
However, despite their success, there are flaws in both SAEs, as well as the theory that seeks to explain it. For one, there are various competing hypotheses about what determines what directions in activation space features should take, which I previously examined. There also seems to be some variation in activation space that cannot be explained by SAEs, and there is some indication that making SAEs wider will not fix this problem.
Sparsity in tensor learning and the global workspace theory
Interestingly, sparsity is not only involved in interpreting neural networks via SAEs, but sparsity is also used in other fields to help understand complex systems. For example, sparsity constraints are added to tensor decomposition methods in biology to help yield more interpretable factors and, ultimately, to better elucidate biological mechanisms (example 1, example 2). I supposed you could argue that these systems exhibit superposition too, and that is what the sparsity is helping with, but I think this is somewhat of a stretch. I think that cross-domain examples point to sparsity as being fundamentally correlated to interpretability in some way.
One way you may be able to look at this is through the lens of Global Workspace Theory (GWT). GWT is a concept from cognitive science that describes the human mind as containing a conscious “theater”, which has a limit to the number of abstractions it can handle at once, often described as 5-7. Abstractions are filtered from other parts of the brain (the global workspace) before entering the theater. I originally learned about GWT through Yoshua Bengio’s writing, for example this paper on The Consciousness Prior (where, btw, involves a sparse factor graph). I relate this to neural network interpretability in the sense that analyzing an entire weight matrix or activation vector as being difficult because of the sheer number of abstractions it contains, and that they don’t fit in the “theater”. Sparsity, then, is about creating fewer abstractions at a higher level that can then fit in the theater.
My question is: what if the main lesson from the success of SAEs is not that linear features in superposition are the fundamental components of neural network operation, but that interpretability is fundamentally related to building sparse, yet faithful, representations of an arbitrary mechanism?
But doesn’t adding hidden layers undermine the point of using SAEs for interpretation? How do we know the influence of each feature?
This is sort of the key point of contention. I think that this is the common implicit assumption that people have and plausibly also why this approach hasn’t been tried. On one hand, to this point, particularly if you’re adding hidden decoder layers, you’re going to lose the advantage of each SAE feature corresponding linearly to a single direction in LLM activation space. But on the other hand, I don’t see this as the important thing that SAEs are used for. SAE use commonly involves (1) identifying the “meaning” or “concept” of an SAE feature by examining its activation patterns across text (2) making predictions about the output of the LLM using the activation of your SAE feature on a new input (3) taking a “causal intervention” approach where you tweak the activation of the SAE feature and see if it has the expected effect on the LLM behavior. And I don’t see in principle why these wouldn’t be viable with deep SAEs.
Yes, this project is a move toward alchemy
If I had to bet, I would say that Zico Kolter would probably classify this approach as falling under the alchemy umbrella. This is because it is a move away from using a concrete underlying theory to more heavily relying on just finding correlations in the data. But I think part of my point is that this isn’t so much of a bad thing (after all, his talk was titled “A lukewarm defense of alchemy”). In essence, the reason I bring it up is that in his talk, the point he roughly made was that people have been searching for these specific mathematical formulations for the workings of neural networks, as if the only valid understanding of neural networks will look like a specific mathematical formulation, such as those we see in theoretical physics, but that he disagrees with the notion that this is the only valid way to understand neural networks. An empirical, more abstract way of thinking (what he calls alchemy) about neural networks is okay too, and that’s all we might be able to achieve. I saw a potential parallel to the current paradigm of SAEs, where people might be overly attributing the success of SAEs to a specific mathematical theory (linear feature superposition) and thus constraining themselves to further approaches that fit within this theory. But we might be able to find more success in succumbing to the alchemy, if you will, and choosing to optimize more for the workflow of SAEs that I described above, even if we no longer have a clean theory to explain why the interpretability works (in other words, we have no way to interpret the interpretability mechanism itself).
Results
If my philosophizing is accurate, this would imply that adding more hidden layers to SAEs would yield more interpretable and faithful explanations of neural network function. So, this is what I’m working on testing.
Deep SAEs on TinyStories
I plan to write up a more thorough manuscript in the coming weeks, but for now I will give a high-level overview of my experiments so far.
Dataset and LLM
First, I trained both shallow and deep SAEs to reconstruct the activations of the TinyStories 3M LLM on the TinyStories dataset. For all of the results in this section, the activations are gathered from the residual stream right before layer 6. To put these activations within a more suitable range, I multiplied them by 10 before passing them to each SAE.
SAE architectures
To create deep SAEs, I added densely connected layers before and, optionally, after the sparse encoding layer. Hidden layers added before the sparse layer used Tanh activations and Layernorms. Hidden layers added after the sparse layer were added before the final decoder layer, which was constrained to have output vectors of unit norm. These hidden decoder layers, contrary to the hidden encoder layers, used ReLUs and no Layernorms, as Layernorms in the hidden decoder layer led to no optimization progress. This may be because of the unit norm constraint of the final decoder layer, which caused the overall scale of the activations in these layers hidden decoder layers to be important. Additionally, a residual connection was added between the input of the SAE and the final encoder layer before the sparse encoder layer, as this seemed to improve optimization significantly. Weight decay was used for every hidden layer (i.e., all layers except the final sparse encoding layer and the final decoder layer), with a weight decay coefficient of 5e-4.
I trained three different model architectures, a standard shallow SAE with a sparse dimension of 256 (2x the dimension of the residual stream), a deep encoder SAE, which included 1 hidden encoder layer with a dimension of 128 and a sparse dimension of 256, and a deep encoder + deep decoder SAE, which included 1 hidden encoder layer with a dimension of 128, a sparse dimension of 256, and 1 hidden decoder layer with a dimension of 128.
Optimization
I used the sparse Adam optimizer, which only updates moment tracking for nonzero gradients, which proved more effective for this sparse optimization problem than Adam, as measured by the number of dead features and the MSE. I used a learning rate of 4e-3 for all models. As the combination of sparse Adam and the extreme simplicity of the TinyStories model caused no dead features to appear throughout training, I did not use feature resampling.
Reconstruction sparsity tradeoff
So far, as per Fig 1, adding hidden layers seems to improve the esteemed L0-MSE frontier, which is a common measure of SAE performance. The MSE scaling is not rescaled at all, so these numbers can’t be directly compared to MSE values for other LLMs. For example, an MSE of 0.32 is actually not very good, which we can see by the fact that the deep encoder SAE achieves this MSE with less than 1 activating latent per input on average.
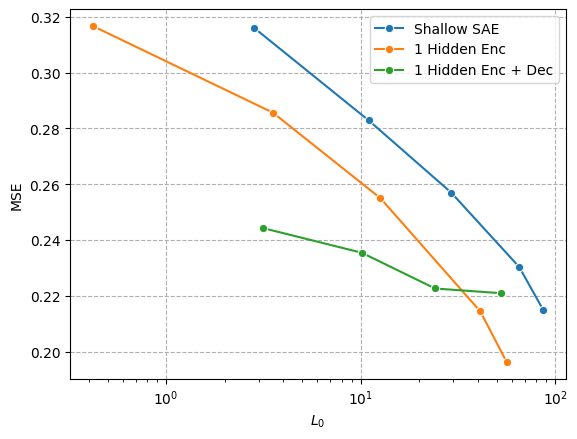
Overall, I think it is expected that deep SAEs will offer an advantage on the sparsity reconstruction frontier, so the real test is whether the features produced by deep SAEs are still interpretable.
Automated interpretability scores
I used the automated SAE interpretability library to generate automated interpretability scores for 3 models, one from each class with similar sparsities (L₀~10). Because of the simplicity of this experiment, I was not expecting to see any advantages to deep SAEs on this test, I just wanted to see if the scores were comparable. There’s also a good chance that the deep SAEs may offer more interpretable features, but that these features are abstract than their shallow SAE counterparts, and so it may require some thought to how to comprehensively test this.
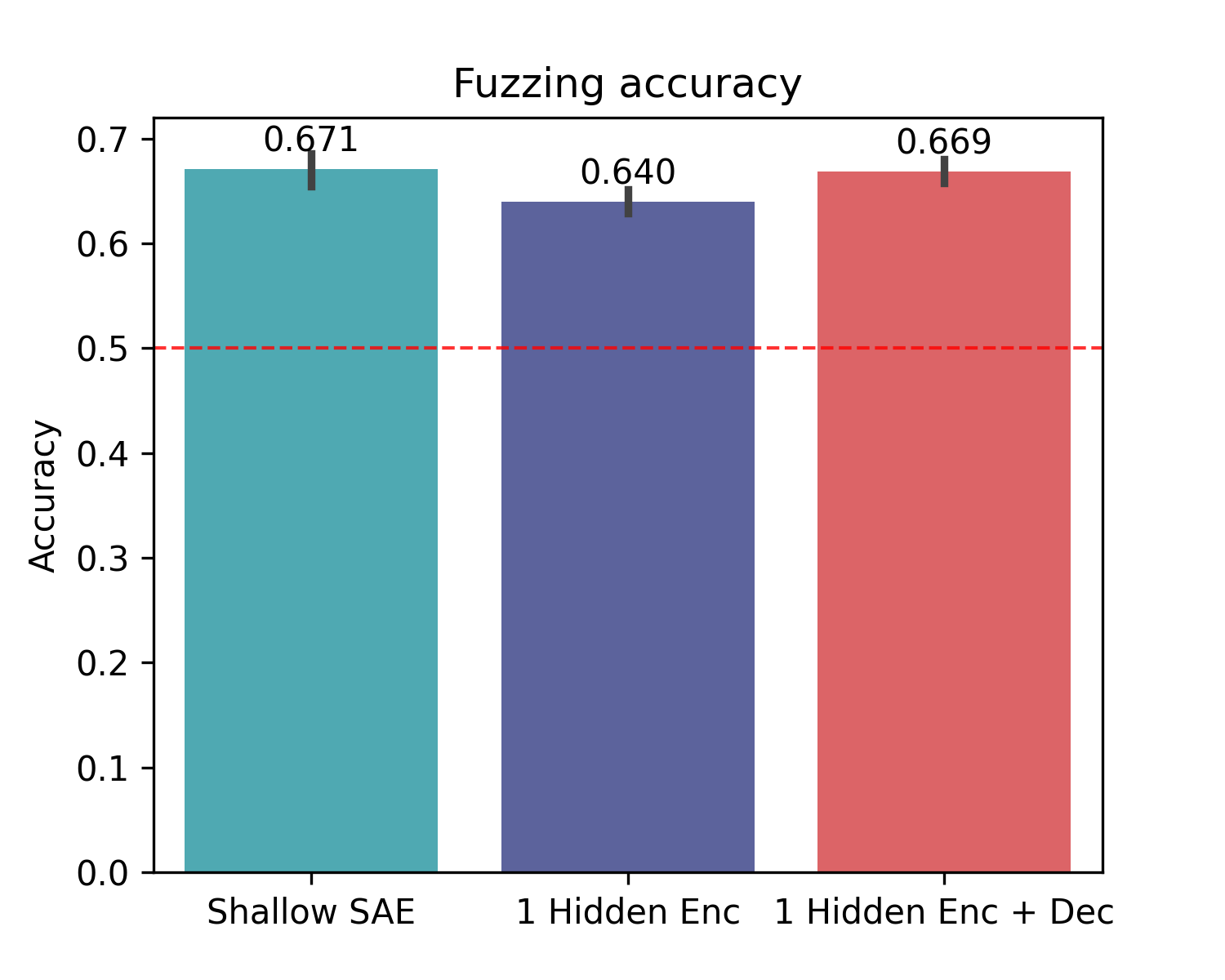
In progress
I’m currently working on scaling this approach up to GPT2.